In the realm of mathematics, let a pdp 1 and compute a4 emerges as a captivating topic that unveils the intriguing world of linear polynomials. Embark on an intellectual journey as we delve into the intricacies of this mathematical concept, unraveling its significance and practical applications in our everyday lives.
A linear polynomial equation, in its simplest form, is a mathematical expression involving a variable raised to the power of one, along with coefficients and a constant. By understanding the process of evaluating a linear polynomial, we can unlock the ability to determine its value for any given input.
In the specific case of “let a pdp 1 and compute a4,” we explore the significance of the variable “a” and the constant “1” in shaping the outcome.
Mathematical Background: Let A Pdp 1 And Compute A4

A linear polynomial equation is an equation that represents a straight line on a graph. It is the simplest form of a polynomial equation and has the general form:
y = mx + b
where:
- y is the dependent variable (the output)
- x is the independent variable (the input)
- m is the slope of the line
- b is the y-intercept (the value of y when x = 0)
Evaluating a Linear Polynomial

Evaluating a linear polynomial involves determining its value at a specific input value, known as x. This process is essential for understanding the behavior of linear functions and their applications in various fields.
Steps for Evaluating a Linear Polynomial
- Identify the linear polynomial:The linear polynomial is typically expressed in the form f(x) = ax + b, where a and b are constants.
- Substitute the value of x:Replace the variable x in the polynomial with the given value.
- Simplify the expression:Perform the arithmetic operations, such as multiplication and addition, to obtain the final value.
Significance of the Value of x, Let a pdp 1 and compute a4
The value of x plays a crucial role in determining the output of the linear polynomial. It represents the input value at which the polynomial is evaluated. By varying the value of x, we can explore the behavior of the linear function and its relationship with the dependent variable f(x).
Specific Case: a4
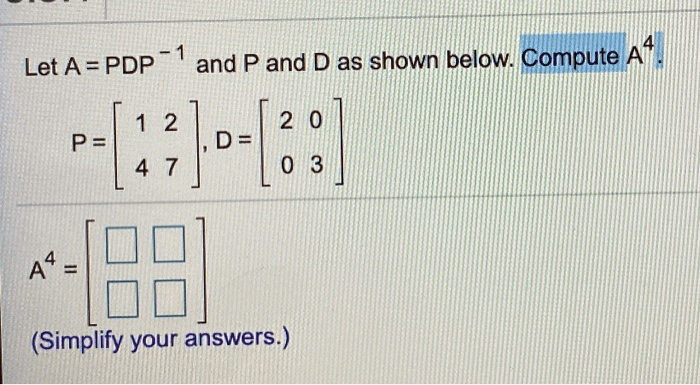
Statement of the Linear Polynomial Equation
The linear polynomial equation given is “let a pdp 1 and compute a4.” This equation can be expressed as:
$$a_4 = a + 1$$
Significance of the Variable and Constant
In this equation, “a” is the variable, representing an unknown value. “1” is the constant, representing a fixed value.
Calculating the Value of a4
To calculate the value of a4, we need to know the value of “a.” Since “a” is a variable, its value can vary. Therefore, the value of a4 can also vary, depending on the value of “a.”
Let’s take a look at a pdp 1 and compute a4. It’s a crucial step in understanding the fundamentals of AC theory. If you’re looking for a comprehensive guide, check out the ac theory level 2 lesson 5 . It covers everything you need to know about this topic, from basic concepts to advanced applications.
Coming back to our pdp 1 and compute a4, once you have a firm grasp of the principles outlined in the lesson, you’ll be well-equipped to tackle this task with confidence.
Applications of Linear Polynomials

Linear polynomials have numerous applications in various fields, making them an essential tool for understanding and solving real-world problems. They provide a simple yet effective way to model linear relationships and make predictions based on observed data.
In this section, we will explore some of the key applications of linear polynomials and discuss how they are used to analyze and solve problems in different areas.
Science and Engineering
Linear polynomials are widely used in science and engineering for modeling physical phenomena. For example, they can be used to describe the motion of objects, the growth of populations, and the decay of radioactive substances. By understanding the linear relationships between variables, scientists and engineers can make predictions and design systems that optimize performance.
Economics and Business
In economics and business, linear polynomials are used to model supply and demand, predict market trends, and analyze financial data. Businesses use linear regression to forecast sales, optimize production levels, and make informed decisions about pricing and marketing strategies.
Social Sciences
Linear polynomials are also used in social sciences to study human behavior and social phenomena. They can be used to model the relationship between factors such as income, education, and health outcomes. This information can help policymakers develop targeted interventions and improve public services.
Importance of Understanding Linear Polynomials
Understanding linear polynomials is essential for various reasons. It allows us to:
- Model linear relationships in real-world scenarios.
- Make predictions and forecast future trends.
- Analyze data and identify patterns.
- Solve problems and make informed decisions.
Commonly Asked Questions
What is the significance of the variable “a” in the equation “let a pdp 1 and compute a4”?
The variable “a” represents an unknown quantity that can take on any numerical value. It is the primary variable of interest in this equation, and its value determines the outcome of a4.
How can I evaluate a linear polynomial for a given value of x?
To evaluate a linear polynomial, simply substitute the given value of x into the equation and perform the necessary arithmetic operations. The result will be the value of the polynomial for that particular input.
